Breadth First Search Algorithm (BFS)

Breadth-first search (BFS) is an algorithm for traversing or searching a graph or tree data structure. It starts at a chosen vertex (or node) of a graph and explores all the neighboring vertices first, then all their neighbors, and so on, until all vertices have been visited. BFS visits the vertices in layers, where a layer is defined as all vertices at the same distance from the starting vertex.

BFS uses a queue data structure to keep track of the vertices to be visited in a first-in-first-out (FIFO) order. The algorithm starts by visiting the starting vertex and adding it to the queue. It then removes the vertex from the front of the queue and visits all of its neighbors, adding them to the back of the queue if they have not been visited yet. This process continues until the queue is empty.

BFS is commonly used in graph algorithms such as finding the shortest path between two vertices, detecting cycles in a graph, or finding all connected components in an undirected graph. It guarantees that the shortest path is found when the graph is unweighted, meaning that all edges have the same weight or cost. In addition, BFS can be used to solve puzzles such as the sliding puzzle and maze traversal.

BFS algorithm

Breadth’s first search in short BFS is a graph traversal algorithm. Graph traversal algorithm means visiting all nodes of a graph.

We will maintain an array let’s say visited. visited[a] means whether node a is visited or not. if a is visited visited[a] is 1 otherwise false.
We will maintain a queue let’s say the queue is q.
The algorithm works as follows

1. We will start this algorithm by putting any nodes at the back of the queue.
2. Assign 1 to the visited array of this node
3. Take the front node from the queue. let’s say it is r.
4. Delete r from the queue
5. Traverse through the adjacency list of node r. If the adjacent node is not visited, put this node at the back of the queue and make this node visited.
6. Repeat from 3 to 5 until the queue is empty

BFS Example

Let’s see how BFS works with an example. We use an undirected graph with 5 nodes

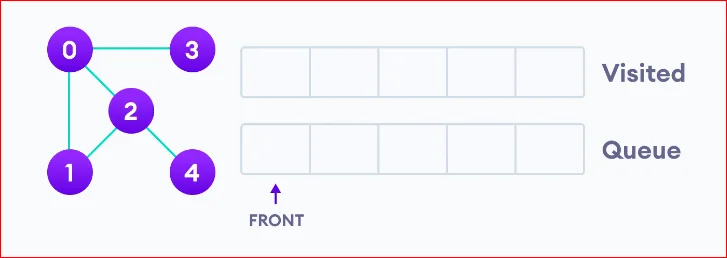
We start from vertex 0, the BFS algorithm starts by putting it in the Visited list and putting all its adjacent vertices in the stack.

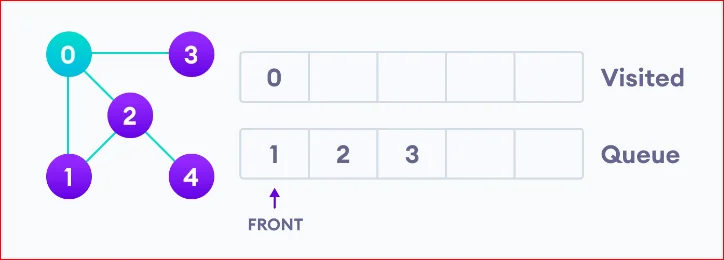
Next, we visit the element at the front of the queue i.e. 1, and go to its adjacent nodes. Since 0 has already been visited, we visit 2 instead.

Vertex 2 has an unvisited adjacent vertex in 4, so we add that to the back of the queue and visit 3, which is at the front of the queue.

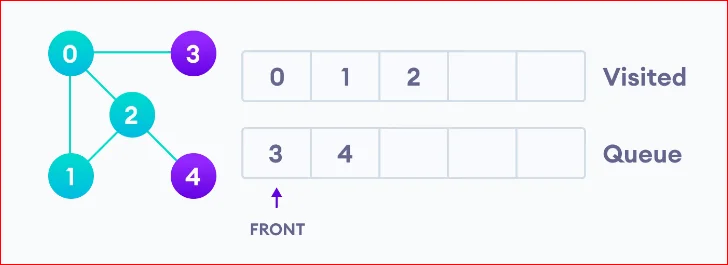
Only 4 remains in the queue since the only adjacent node of 3 i.e. 0 is already visited. We visit it.

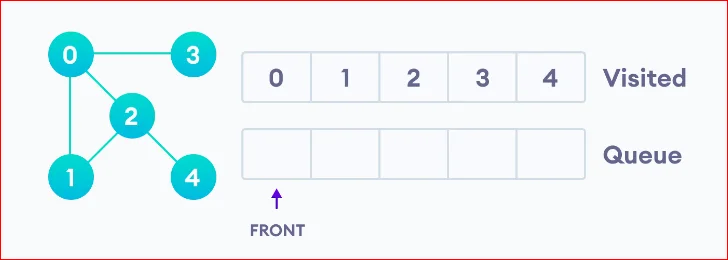
Since the queue is empty, we have completed the Breadth First Traversal of the graph.

BFS pseudocode

create a queue Q 
mark v as visited and put v into Q 
while Q is non-empty 
    remove the head u of Q 
    mark and enqueue all (unvisited) neighbours of u

BFS in C++

//#include<bits/stdc++.h>
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main()
{
	int n,m;
	cin>>n; // n is the number of vertices
	cin>>m; // m is the number of edges
	vector<vector<int> > adj(n); // n vector for each node

	// input edgelist
	for(int i=0;i<m;i++)
	{
		int a, b;
		cin>>a>>b;
		adj[a].push_back(b);
		adj[b].push_back(a);
	}
	vector<int> visited(n);
	queue<int> q;
	q.push(0);
	visited[0]=1;
	while(!q.empty())
	{
		int r=q.front();
		q.pop();
		cout<<r<<' ';
		for(auto it:adj[r])
		{
			if(visited[it]==0) q.push(it);
			visited[it]=1;
		}
	}
	cout<<endl;

	return 0;
}

This is a C++ program for Breadth First Search (BFS) traversal of an undirected graph, represented using an adjacency list.

Here’s a brief explanation of the code:

• The program takes the input of the number of vertices (n) and the number of edges (m).

• It creates a vector of vectors ‘adj’, where each vector in the vector represents the adjacency list for a particular vertex.

• The program then takes the input from the edge list and updates the adjacency list accordingly. Note that the graph is undirected, so for every edge (a,b), we add b to the adjacency list of a and a to the adjacency list of b.

• A vector ‘visited’ of size n is created and initialized to 0. This vector is used to keep track of the vertices that have been visited during the BFS traversal.

• A queue ‘q’ is initialized with the starting vertex (vertex 0) and visited[0] is set to 1.

• The while loop runs until the queue is empty. In each iteration, it pops the front element ‘r’ from the queue and prints it.

• For each adjacent vertex ‘it’ of ‘r’, if it hasn’t been visited yet, it is added to the queue and visited[it] is set to 1.

• The program ends after all vertices have been visited.

Note: The header file ‘bits/stdc++.h’ is not a standard C++ header file and is not recommended for use in competitive programming. It includes a lot of other header files, which can lead to slower compilation times. Instead, it’s better to include only the required header files.

BFS in Python

from collections import deque 
adj=[]
n=int(input()) # number of vertices.
m=int(input()) # number of edges
 
 
for i in range(n):
    adj.append([])
 
 
# input edge list.
for i in range(m):
    a, b=map(int, input().split())
    adj[a].append(b)
    adj[b].append(a)
     

dq=deque([0])
visited=[0 for i in range(n)]
visited[0]=1
while dq:
	r=dq[0]
	dq.popleft()
	print(r, end=' ')
	for i in adj[r]:
		if visited[i]==0:
			visited[i]=1
			dq.append(i)

This is a Python program for Breadth First Search (BFS) traversal of an undirected graph, represented using an adjacency list.
Here’s a more detailed explanation of the code:

• The program starts by taking input from the number of vertices (n) and the number of edges (m) of the undirected graph.

• It initializes an empty list ‘adj’ with n empty lists. This list will be used to store the adjacency list of each vertex.

• The program then takes the input from the edge list and updates the adjacency list accordingly. For each edge (a,b), it adds b to the adjacency list of a and a to the adjacency list of b.

• The program initializes a deque (double-ended queue) ‘dq’ with the starting vertex (vertex 0) and initializes a list ‘visited’ of size n with all elements set to 0. The ‘visited’ list will be used to keep track of the vertices that have been visited during the BFS traversal.

• It sets visited[0] to 1 to indicate that the starting vertex has been visited.

• The while loop runs until the deque is empty. In each iteration, it pops the leftmost element ‘r’ from the deque and prints it.

• For each adjacent vertex ‘i’ of ‘r’, if it hasn’t been visited yet, it is added to the deque, and visited[i] is set to 1.

• The program continues this process until all vertices have been visited.

The program performs BFS traversal of an undirected graph using an adjacency list and a deque data structure to keep track of the vertices to be visited. The visited vertices are marked using a visited list.